
Прямоугольник — это особый вид четырехугольника, который обладает рядом особенностей. Во-первых, все его углы равны 90 градусов, что делает его геометрическую форму похожей на прямой угол. Во-вторых, противоположные стороны прямоугольника параллельны и равны между собой. Также в прямоугольнике все внутренние углы равны 90 градусов.
Прямоугольник является одной из основных и наиболее известных геометрических фигур. Его длинные стороны называются прямыми, а короткие — поперечными. Также прямоугольник может иметь дополнительные свойства, например, равные диагонали или симметричность относительно своих сторон.
Прямоугольники широко используются в различных областях, включая архитектуру, инженерию, графику, конструирование и многие другие. Их простота и симметрия делают их удобными для измерений, расчетов и построений. Кроме того, прямоугольники являются основой для многих других геометрических фигур, таких как квадраты и параллелограммы.
Что такое прямоугольник
Прямоугольник – это особый вид четырехугольника, у которого все углы прямые (равны 90°). Прямоугольник имеет четыре стороны, две из которых параллельны и равны между собой, а другие две стороны также параллельны друг другу и тоже равны. Прямоугольник получает свое название из-за свойства иметь прямые углы.
Прямоугольники являются одной из самых изученных и применяемых форм в математике и геометрии. Их широко используют при решении задач, в строительстве, дизайне и других областях, где важно учитывать геометрические пропорции и правильность формы.
Если в прямоугольнике все четыре стороны равны, то он называется квадратом. Квадрат также является прямоугольником, но имеет дополнительное свойство – все стороны у него равны и все углы прямые.
Прямоугольники могут иметь различные размеры и пропорции. Большая или маленькая, широкая или узкая форма – все они являются прямоугольниками, если углы прямые и стороны параллельны и равны друг другу.
| Типы прямоугольников | Описание |
|---|---|
| Прямоугольник в широком смысле | Прямоугольник с различными размерами и пропорциями сторон. |
| Квадрат | Прямоугольник, у которого все стороны равны. |
| Прямоугольник в узком смысле | Прямоугольник, у которого две стороны параллельны и равны, а другие две стороны также параллельны и равны. |
Прямоугольник – это важная геометрическая фигура, которая находит свое применение во многих областях. Знание о прямоугольниках и их свойствах позволяет анализировать и решать различные задачи, а также создавать эстетически приятные и гармоничные формы в дизайне и архитектуре.
Определение прямоугольника
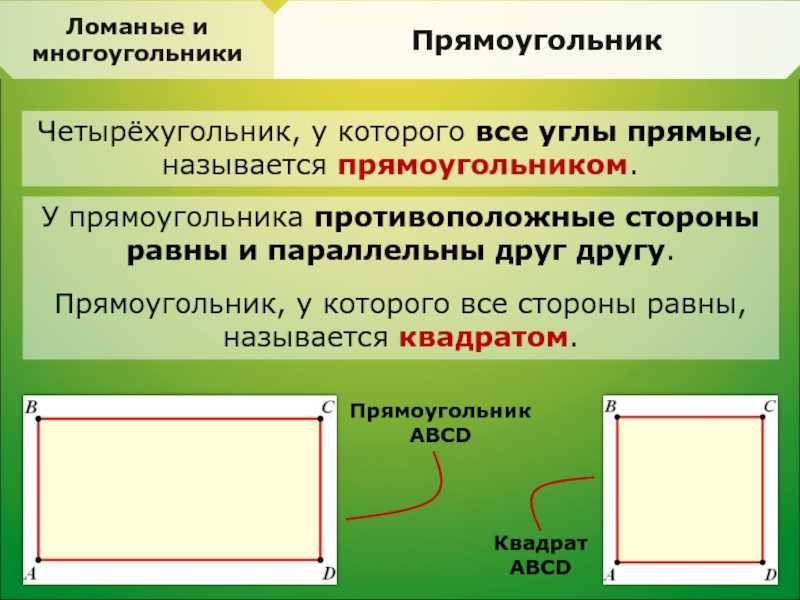
Прямоугольник — это особый вид четырехугольника, у которого все углы равны 90 градусам. Он имеет две пары параллельных сторон, которые пересекаются под прямым углом. Параллельные стороны прямоугольника называются его сторонами, а перпендикулярные стороны — его высотой и шириной.
Прямоугольник является простейшей и наиболее распространенной фигурой в геометрии. Он обладает рядом важных свойств, которые делают его удобным для использования в различных областях. Например, прямоугольники широко применяются в архитектуре и строительстве, дизайне и изобразительном искусстве, графике и компьютерной графике, математике и физике, а также в повседневной жизни.
Прямоугольники могут быть разного размера и пропорции. Однако, все они сохраняют свои основные характеристики: углы, параллельные стороны и соотношение между сторонами. Если все стороны прямоугольника равны, то он называется квадратом.
Прямоугольники обладают рядом важных свойств и формул. Например, площадь прямоугольника вычисляется по формуле: площадь = длина x ширина. Периметр прямоугольника вычисляется по формуле: периметр = 2 x (длина + ширина).
Свойства прямоугольника
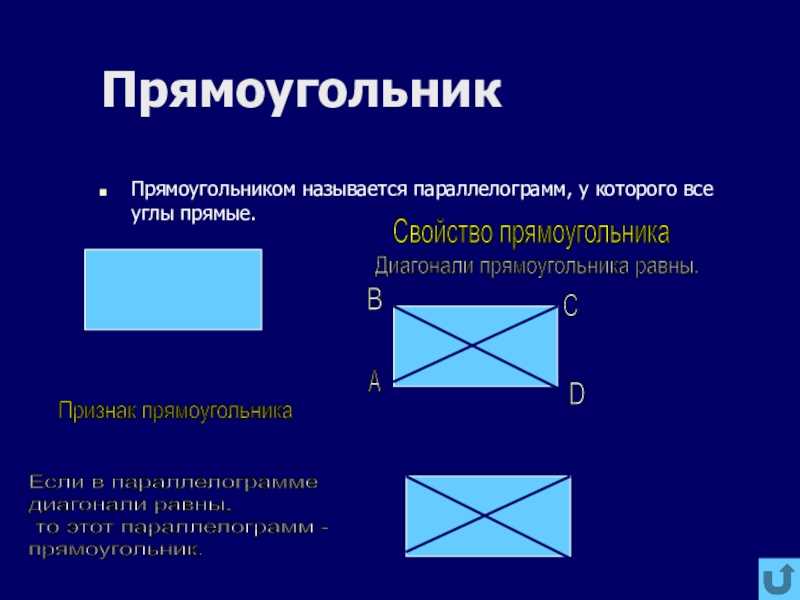
Прямоугольник — это четырехугольник, у которого противоположные стороны попарно равны и все углы прямые.
Основные свойства прямоугольника:
- У прямоугольника есть две пары параллельных сторон, которые называются боковыми сторонами и основаниями.
- Боковые стороны прямоугольника равны между собой и параллельны.
- Основания прямоугольника также равны между собой и параллельны.
- У прямоугольника четыре угла, которые равны между собой и прямы.
- Диагонали прямоугольника равны между собой и делят прямоугольник на два прямоугольных треугольника.
Формулы для вычисления свойств прямоугольника:
- Площадь прямоугольника равна произведению длин его сторон: П = a * b, где a и b — длины сторон прямоугольника.
- Периметр прямоугольника равен удвоенной сумме длин его сторон: 2 * (a + b).
- Длина диагонали прямоугольника может быть найдена по теореме Пифагора: диагональ² = a² + b², где a и b — длины сторон прямоугольника.
Примеры использования:
| Свойство | Значение |
|---|---|
| Стороны | AB = CD = 5 см BC = AD = 3 см |
| Углы | Угол A = Угол B = Угол C = Угол D = 90° |
| Площадь | П = 5 см * 3 см = 15 см² |
| Периметр | P = 2 * (5 см + 3 см) = 16 см |
| Длина диагонали | диагональ² = 5 см² + 3 см² = 34 см² Диагональ ≈ √34 см |
Как отличить прямоугольник от других четырехугольников
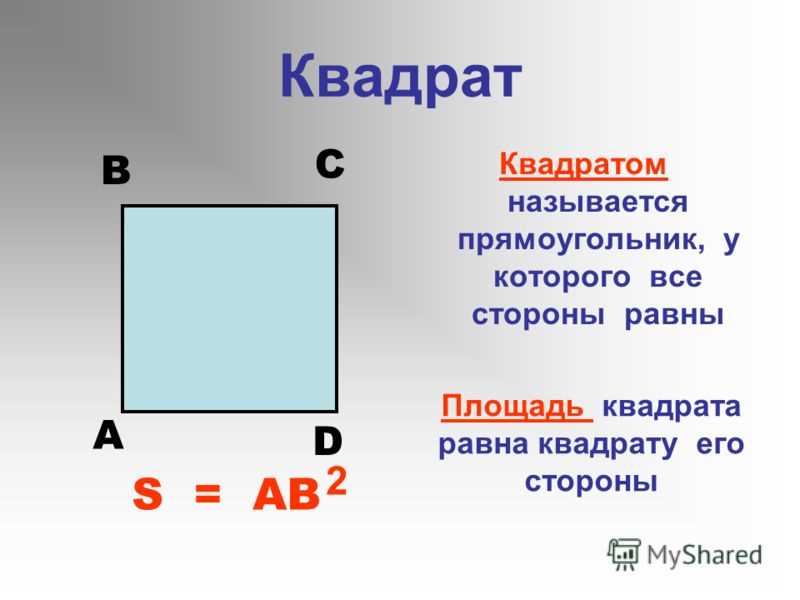
Прямоугольник — это особый вид четырехугольника, который имеет определенные характеристики и свойства. Для того чтобы отличить прямоугольник от других четырехугольников, необходимо обратить внимание на следующие признаки:
- Углы: Прямоугольник имеет четыре угла, все из которых равны по 90 градусов. Это значит, что все углы прямоугольника являются прямыми.
- Стороны: В прямоугольнике противоположные стороны равны друг другу и параллельны. То есть, две противоположные стороны прямоугольника равны между собой, а остальные две стороны тоже равны друг другу.
- Диагонали: Диагонали прямоугольника имеют одинаковую длину и пересекаются под прямым углом в центре прямоугольника.
- Свойства: Прямоугольник обладает свойствами, которые не присущи другим четырехугольникам. Например, прямоугольник можно разделить на два равных треугольника по диагонали, а его периметр равен сумме длин всех четырех сторон.
Если четырехугольник обладает всеми вышеперечисленными признаками, то он является прямоугольником. Будьте внимательны при определении фигуры, чтобы не спутать прямоугольник с другими четырехугольниками, такими как параллелограмм или ромб.
Углы прямоугольника
Прямоугольник — это четырехугольник, у которого все углы равны 90 градусам. Углы прямоугольника играют ключевую роль при определении его свойств и характеристик.
В прямоугольнике имеется четыре угла:
- Угол A: расположен в левом верхнем углу.
- Угол B: находится в правом верхнем углу.
- Угол C: находится в правом нижнем углу.
- Угол D: расположен в левом нижнем углу.
Все эти углы имеют одинаковую меру и равны 90 градусам. Это означает, что каждый угол прямоугольника является прямым углом.
Углы прямоугольника имеют важное значение при вычислении его периметра и площади. Также углы определяют степень его вращения и выравнивают его стороны.
Стороны прямоугольника

Прямоугольник — это четырехугольник, у которого все углы прямые.
У прямоугольника есть две параллельные стороны, которые называются основаниями, и две стороны, которые называются боковыми сторонами. Основания прямоугольника обычно обозначаются буквами «а» и «b», а боковые стороны — буквами «с» и «d».
Строго говоря, у прямоугольника нет противоположных сторон, поскольку все его стороны являются параллельными и образуют прямые углы. Однако, в контексте сравнения сторон прямоугольника, можно говорить о парах противоположных сторон. Так, основания «а» и «b» являются противоположными сторонами, а также стороны «с» и «d».
Для прямоугольника характерны следующие особенности:
- Основания прямоугольника параллельны и равны между собой (а = b).
- Боковые стороны прямоугольника также параллельны друг другу и равны между собой (с = d).
- Противоположные стороны прямоугольника перпендикулярны друг другу (все углы прямые).
- Длина сторон прямоугольника может быть различной.
Стороны прямоугольника можно измерять в любых единицах длины, например в сантиметрах, метрах, футах или дюймах.
Диагонали прямоугольника
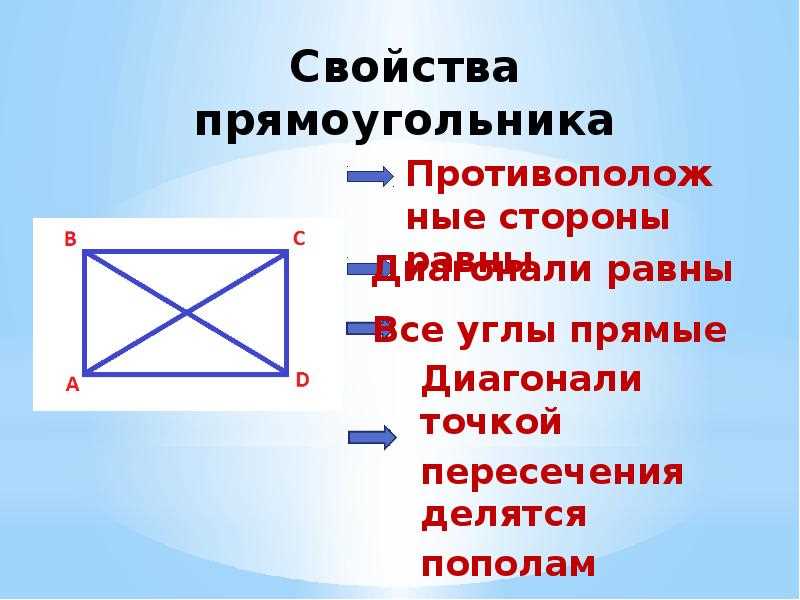
Прямоугольник — это четырехугольник, у которого противоположные стороны равны и параллельны, а углы прямые.
Диагонали прямоугольника — это отрезки, соединяющие противоположные вершины этой фигуры. Прямоугольник имеет две диагонали: главную и побочную.
Главная диагональ является длиннейшей диагональю прямоугольника и делит его на два равных треугольника. Длина главной диагонали равна √(a² + b²), где a и b – длины сторон прямоугольника.
Побочная диагональ является второй диагональю прямоугольника и делит его на два равных треугольника. Длина побочной диагонали также равна √(a² + b²), где a и b – длины сторон прямоугольника.
Главная и побочная диагонали прямоугольника пересекаются в точке, которая является центром симметрии фигуры.
Прямоугольник — это одна из самых распространенных геометрических фигур, чьи диагонали играют важную роль при решении различных задач и вычислений.













