
Компьютер – это сложное устройство, которое состоит из множества компонентов и выполняет различные функции. Для того чтобы понять, как работает компьютер и какие принципы его функционирования лежат в его основе, необходимо обратиться к формальной модели компьютера.
Формальная модель компьютера – это абстрактное представление устройства, которое позволяет описать его работу с точки зрения математических операций. Она упрощает понимание принципов работы компьютера и позволяет строить решения на его основе.
Одной из самых распространенных формальных моделей компьютера является модель фон Неймана. Согласно этой модели, компьютер состоит из памяти, центрального процессора, устройств ввода-вывода и системы управления. Она представляет собой последовательность команд, которые выполняются в строгом порядке.
Важно понимать, что формальная модель компьютера не ограничивается только моделью фон Неймана. Существуют и другие модели, которые могут использоваться для описания различных типов компьютеров. Но, независимо от выбранной модели, она позволяет лучше понять устройство компьютера и принципы его работы.
Классификация компьютерных моделей

В мире существует множество различных компьютерных моделей, каждая из которых имеет свои особенности и применение. В данной статье рассмотрим основные классификации компьютерных моделей.
1. Разделение по назначению:
- Пользовательские компьютеры — предназначены для использования конечными пользователями в повседневных задачах. Это настольные компьютеры, ноутбуки, планшеты и смартфоны.
- Серверы — предоставляют службы и ресурсы другим компьютерам в сети. Используются для хранения и обработки данных, веб-хостинга, облачных вычислений и др.
- Рабочие станции — предназначены для выполнения специфических задач, требующих высокой производительности, например, в графическом дизайне, инженерии и видеомонтаже.
- Мобильные устройства — предназначены для передвижного использования и включают в себя смартфоны, планшеты и ноутбуки.
2. Разделение по архитектуре:
- x86 — широко распространенная архитектура, используемая в большинстве персональных компьютеров.
- ARM — архитектура, используемая в большинстве мобильных устройств.
- SPARC — архитектура, используемая в серверах и рабочих станциях, разработанных Oracle.
- PowerPC — архитектура, используемая в системах IBM и Apple до перехода на процессоры Intel.
3. Разделение по размеру и мощности:
- Суперкомпьютеры — самые мощные и дорогостоящие компьютеры, используемые в научных и инженерных расчетах, моделировании погоды, криптографии и др.
- Мейнфреймы — крупные компьютеры, способные обрабатывать огромные объемы данных и обслуживать большое количество пользователей одновременно.
- Мини-компьютеры — компактные компьютеры средней мощности, используемые в бизнесе и научных исследованиях.
- Рабочие станции — компьютеры с высокой производительностью, предназначенные для специализированных задач.
- Ноутбуки и настольные компьютеры — наиболее распространенный тип компьютеров в повседневном использовании.
4. Разделение по операционной системе:
- Windows — операционная система от Microsoft, наиболее распространенная в мире.
- macOS — операционная система для компьютеров Apple.
- Linux — свободная и открытая операционная система, используемая в большом количестве серверов и рабочих станций.
- iOS — мобильная операционная система для устройств Apple.
- Android — мобильная операционная система для большинства смартфонов и планшетов.
5. Разделение по производителю:
Компьютерные модели производятся различными компаниями, такими как Apple, Dell, HP, Lenovo, Asus, Samsung и др. Каждый производитель имеет свои уникальные модели, которые могут отличаться по дизайну, функциональности и техническим характеристикам.
Это лишь некоторые из возможных классификаций компьютерных моделей. Каждая модель имеет свои преимущества и недостатки, и выбор определенной модели зависит от потребностей и задач пользователя.
Формальные модели
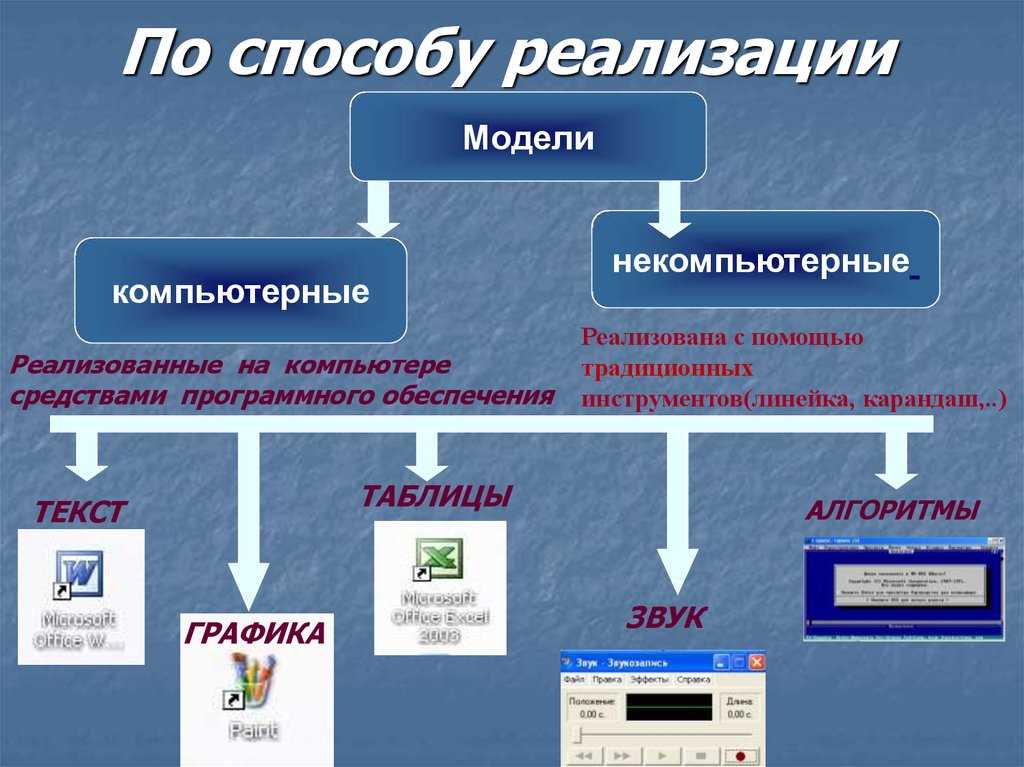
Формальные модели являются математическими абстракциями, которые используются для описания и анализа различных систем и процессов. Они позволяют более точно и формально изучать объекты и явления, применять логические рассуждения и выводы, а также предсказывать и контролировать результаты.
В контексте компьютерных наук и информатики формальные модели используются для описания компьютерных систем, аппаратуры и программного обеспечения. Они помогают разработчикам и исследователям лучше понять принципы работы компьютера, выявить и исправить ошибки, а также разработать новые алгоритмы и методы обработки данных.
Формальные модели компьютера могут быть представлены в виде математических структур, графов, деревьев и таблиц, которые описывают различные аспекты компьютерных систем. Например, модель вычислительной машины может содержать информацию о процессоре, памяти, вводе-выводе, а также о взаимодействии между ними.
Одной из наиболее известных формальных моделей компьютера является машина Тьюринга. Она представляет собой абстрактную вычислительную устройство, способное выполнять последовательные операции над символами на бесконечной ленте. Машина Тьюринга используется для формализации понятия алгоритма и вычислений, а также для изучения различных классов задач, включая разрешимость и сложность.
Другой известной формальной моделью компьютера является булева схема. Она представляет собой абстракцию логической схемы, состоящей из логических элементов, таких как И, ИЛИ, НЕ и т.д. Булевы схемы используются для моделирования и анализа работы цифровых схем и логических устройств, а также для разработки и оптимизации логических алгоритмов и систем.
Все формальные модели компьютера имеют свои ограничения и предположения, но они позволяют исследователям и разработчикам более точно и формально описывать и анализировать компьютерные системы. Они являются основой для разработки новых технологий, алгоритмов и приложений, а также для обучения и обучения студентов и специалистов в области компьютерных наук.
Нечеткие модели
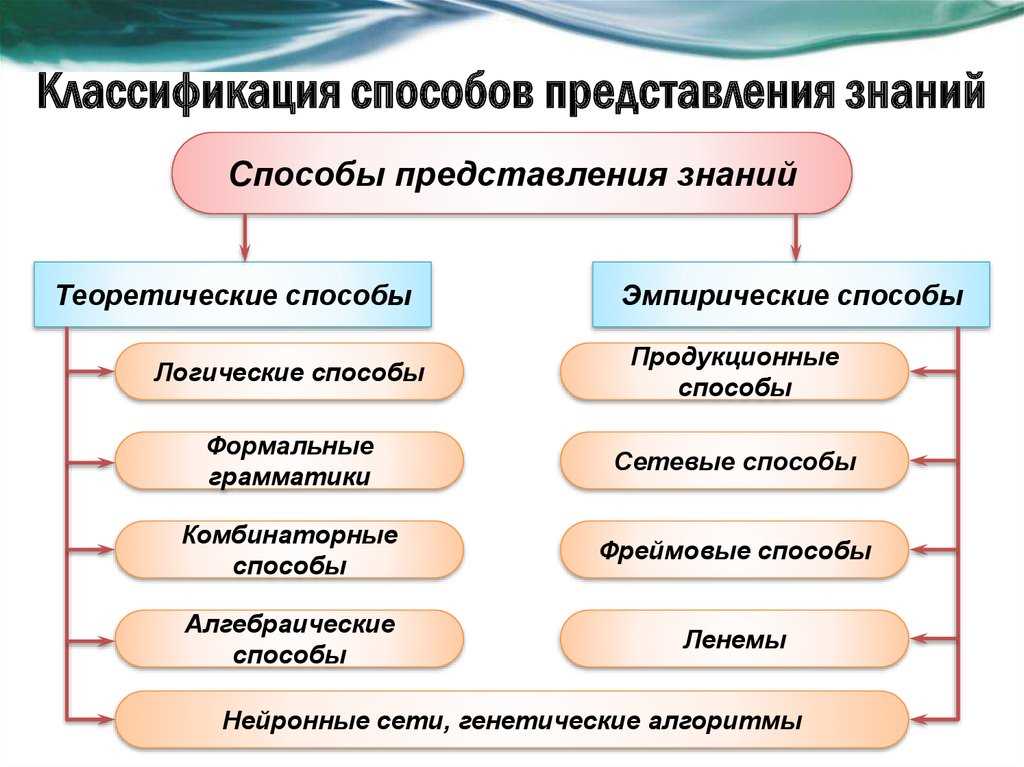
Нечеткие модели – это особый вид математических моделей, которые используются для описания нечетких или неопределенных данных. Они представляют собой расширение традиционных математических моделей, которые работают только с точными значениями.
Основной идеей нечетких моделей является то, что нечеткие или неопределенные данные могут быть описаны и работать с ними можно не только через точные значения, но и с помощью нечетких множеств и нечетких логических операций. Таким образом, нечеткие модели позволяют учитывать неопределенность и нечеткость данных, что делает их более реалистичными и применимыми в реальном мире.
Одним из наиболее распространенных применений нечетких моделей является обработка нечеткой информации. Нечеткость может возникать, например, при оценке качества товара или при принятии решений на основе нечетких критериев. Нечеткие модели позволяют учесть различные факторы и неопределенность данных, что делает их более гибкими и применимыми в таких ситуациях.
В нечетких моделях для описания данных используются нечеткие множества. Нечеткое множество – это множество, элементы которого имеют разную степень принадлежности к данному множеству. Степень принадлежности определяется нечеткой функцией принадлежности, которая может принимать значения от 0 до 1.
Для работы с нечеткими моделями используются различные методы и алгоритмы, которые позволяют решать задачи на основе нечетких данных. Например, нечеткая логика, нечеткие алгоритмы кластеризации и классификации, нечеткие системы управления и т.д.
Нечеткие модели находят широкое применение в различных областях, таких как искусственный интеллект, экспертные системы, теория принятия решений, управление, планирование, прогнозирование и др. Благодаря своей способности работать с нечеткими данными, нечеткие модели позволяют создавать более гибкие и адаптивные системы, способные адекватно реагировать на изменения в окружающей среде и неопределенность данных.
Статистические модели
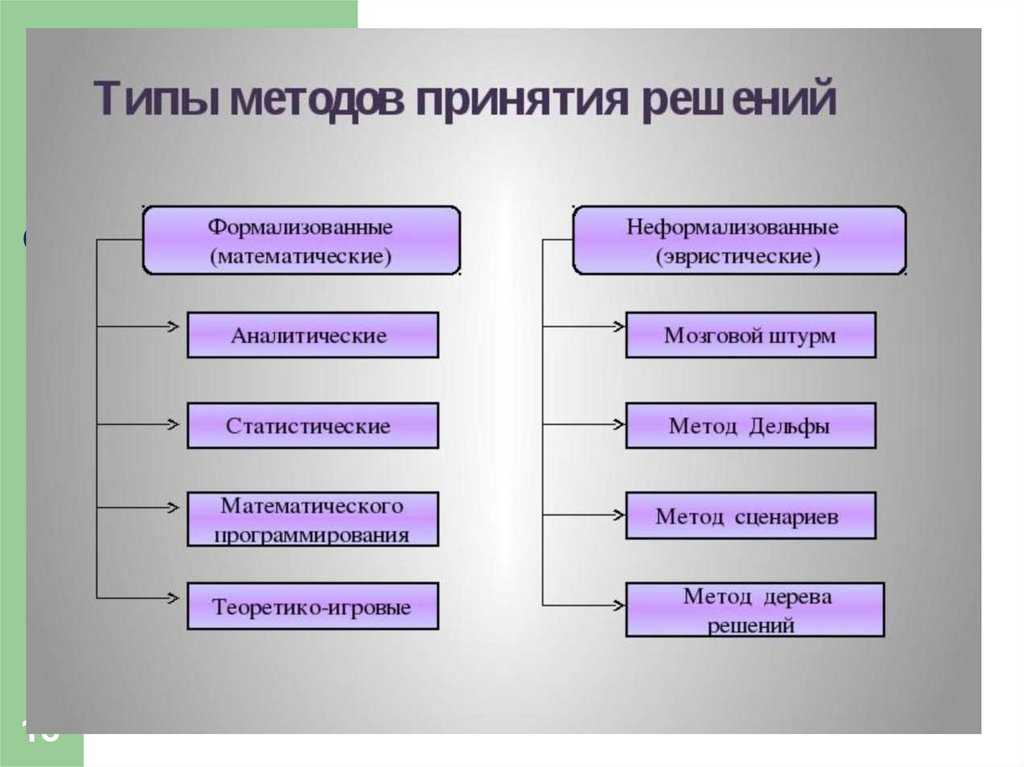
Статистические модели представляют собой математические модели, основанные на статистических данных и вероятностных распределениях. Они используются для описания и объяснения различных явлений, основываясь на наблюдаемых данных.
Статистические модели могут быть применены во многих областях, включая экономику, физику, медицину, социологию и многие другие. Они позволяют исследователям проводить статистический анализ данных, выделять важные закономерности и находить связи между переменными.
Основные компоненты статистических моделей включают:
- Переменные: это значения, которые варьируются в зависимости от наблюдаемых данных. В статистических моделях переменные могут быть как непрерывными, так и дискретными.
- Параметры: это значения, которые описывают свойства статистической модели. Они могут быть известными или неизвестными и подлежать оценке на основе имеющихся данных.
- Функция распределения: это математическая функция, которая описывает вероятность различных значений переменных. Она является основным инструментом статистических моделей.
Статистические модели могут быть простыми или сложными, в зависимости от количества и связи переменных. Они могут использовать различные методы и подходы, такие как линейная регрессия, логистическая регрессия, временные ряды, анализ выживаемости и другие.
Использование статистических моделей позволяет исследователям делать выводы на основе статистической значимости, проводить прогнозирование и принимать решения на основе анализа данных. Они позволяют более точно понимать и объяснять сложные явления и процессы, а также помогают сделать предсказания и определить риски и возможности.
В целом, статистические модели являются важным инструментом для анализа данных и исследования различных явлений. Они помогают нам лучше понимать мир вокруг нас и принимать обоснованные решения на основе вероятностных распределений и статистических закономерностей.
Определение формальных моделей

Формальные модели представляют собой математические или логические конструкции, которые используются для описания и анализа систем, процессов или явлений в строгом формальном виде. Они помогают упростить и абстрагировать сложные реальные ситуации и представить их в виде четких правил и закономерностей.
Формальные модели широко применяются в различных областях знаний, таких как математика, физика, информатика, экономика, социология и другие. Они позволяют проводить анализ системы на основе строгих математических методов, предсказывать ее поведение, оптимизировать работу и принимать обоснованные решения.
Формальные модели могут быть представлены в различных форматах, включая графические, алгоритмические, математические и логические. Они обладают определенными свойствами, такими как точность, строгость, формальность, их можно проверять на корректность и использовать для доказательства теорем.
Примеры формальных моделей:
- Логические модели, основанные на формальной логике, такие как таблицы истинности и логические уравнения.
- Математические модели, включающие дифференциальные уравнения, теорию вероятности, линейное программирование и другие математические методы.
- Графические модели, такие как блок-схемы, диаграммы состояний, UML-диаграммы и другие графические инструменты.
- Алгоритмические модели, представленные в виде алгоритмов и программного кода.
Использование формальных моделей позволяет получить более глубокое понимание сложных систем и явлений, а также предоставляет возможность проводить анализ, оптимизацию и управление ими.
Что такое формальная модель
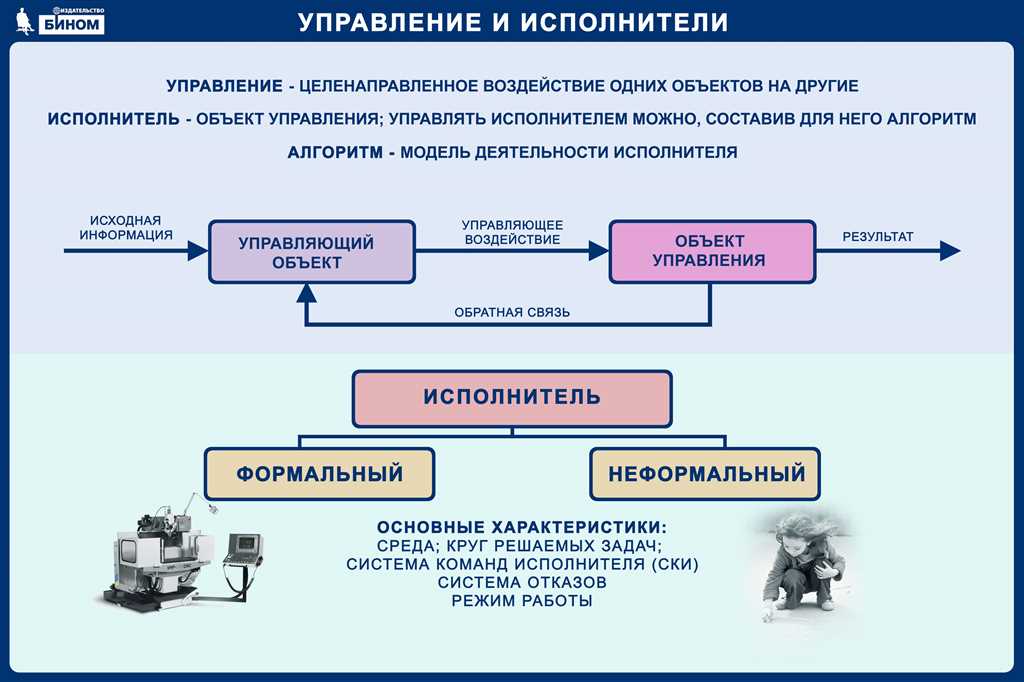
Формальная модель — это абстрактный математический объект, который используется для описания и анализа реального объекта или системы. Она представляет собой формальное представление, которое позволяет наглядно описать структуру и функциональность объекта или системы.
Формальные модели широко применяются в различных областях, таких как информатика, математика, физика, инженерия и др. Они являются важным инструментом для исследования и проектирования сложных систем.
В компьютерной науке формальные модели используются для описания аппаратных и программных компонентов компьютера. Они позволяют разработчикам лучше понять и предсказать поведение системы, а также упрощают процесс разработки и тестирования новых технологий и программного обеспечения.
Формальные модели могут быть представлены в виде математических уравнений, диаграмм, таблиц, графов и других абстрактных структур. Они могут быть описаны с помощью языков программирования или специальных формальных языков.
Примеры формальных моделей в компьютерной науке включают в себя логические модели, графовые модели, модели вычислений, модели баз данных и многие другие.
Формальные модели помогают разработчикам исследовать и анализировать сложные системы, предсказывать их поведение, выявлять потенциальные проблемы и улучшать их производительность. Они являются ключевым инструментом в разработке новых технологий и программного обеспечения, а также в улучшении уже существующих.
Цель использования формальных моделей
Формальные модели являются важным инструментом в различных областях науки и техники, включая компьютерные науки, математику, экономику и физику. Они позволяют представить сложные системы и явления в упрощенной форме, что облегчает их изучение и анализ. Вот основные цели использования формальных моделей:
- Понимание системы: формальные модели помогают лучше понять структуру и функционирование сложных систем. Они позволяют выделить основные компоненты системы и определить взаимосвязи между ними.
- Анализ и прогнозирование: формальные модели позволяют проводить анализ системы и предсказывать ее поведение в различных условиях. Они позволяют проверять различные гипотезы и прогнозировать результаты изменений параметров системы.
- Оптимизация: формальные модели помогают оптимизировать работу системы и выявлять ее слабые места. Они позволяют исследовать различные альтернативы и выбрать наилучший вариант для достижения желаемого результата.
- Коммуникация: формальные модели облегчают коммуникацию между специалистами разных областей. Они позволяют представить систему в универсальном формате, который понятен всем участникам проекта, и снижают вероятность недоразумений и ошибок.
В целом, использование формальных моделей позволяет более глубоко изучать и понимать сложные системы, анализировать и прогнозировать их поведение и принимать обоснованные решения на основе полученных результатов. Это важный инструмент для развития науки, техники и технологий в целом.













